Introduction
CatBoost is an open-sourced gradient boosting library that natively handles categorical features and performs well in comparison to existing publicly available implementations of gradient boosting such as XGBoost, LightGBM and H2O. [1]
In this article we present the details of CatBoost’s ordered target-based statistic (ordered TBS), its analytical solution when number of permutations approaches infinity and a lightweight alternative for converting categorical features to numeric.
Overview of the CatBoost ordered TBS
Unlike traditional method of converting categorical features to numeric during data preprocessing, CatBoost’s approach is to deal with them during training just before each split is selected in the tree. The method of transforming categorical features to numeric generally includes the following stages:
- Permuting the set of input objects in a random order. Multiple random permutations are generated.
- Converting the label value from a floating point to an integer (quantization of continuous values in a regression problem).
- Transforming categorical features of each permutation to numerical features. Finally, take the mean of permutations to get the final value of an input object. [2]
As a result, each categorical feature value or feature combination value is assigned a numerical feature. The target-based statistic uses multiple random permutations to avoid overfitting and reduce the high variance of examples with short history [3,5]. Below is an example used also by CatBoost of the results of the transformation (using buckets).
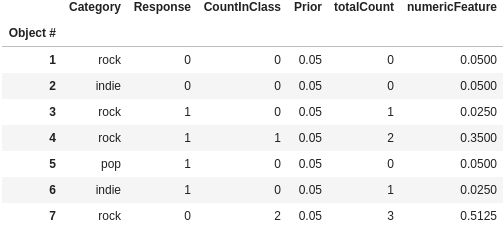
Notice how objects #1 and #7 have the same category and response but very different numeric feature value. Taking mean over multiple permutations reduces this variation. However, if too many permutations are taken, overfitting occurs: in the above example the rock category objects with zero response converge around 0.3455 and those with one around 0.1858. This is the same problem encountered by leave-one-out TBS and alleviated by k-fold/hold-out TBS.
Number of permutations is yet another hyperparameter to tune, although authors claim that two to five iterations before each split should suffice [4]. Additionally the process is computationally more complex than e.g. leave-one-out (LOO) TBS.
Analytical solution to CatBoost’s ordered TBS
The quest for analytical solution starts with the recognition that the last observation’s response is never accounted for. Thus, if the last observation’s response is one (in a binary classification task), the observations get the same numeric values as in the case where number of ones if one less and the last observation’s response was zero. Thus, it suffices to solve the case where the last observation’s value is zero.
As the number of permutations increase, the more “positions” in the dataset a single observation “visits”. As the number of permutations approaches infinity, each position gets visited as often. Thus, we must consider each possible position of each permutation with equal weight.
Let us continue with the rock category introduced earlier. There we have four observations with two positive responses (ones) and two negative (zeros). When the last observation is zero, three unique permutations of responses remain: 0110, 1010 and 1100. With prior P, the observations receive the following numeric values:

Taking the mean of the last row and setting P = 0.05, we get
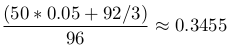
which is the expected value of the elements with zero response in category of size four and two positive responses. Performing similar calculations to different group sizes and positive response counts a pattern emerges. Denote category size with N and the number of positive responses with k. Then, the expected value of the zero response observations of a given group is

Notice the last line: it is the formal presentation of the observation presented at the beginning of this section.
Alternative TBS for categorical variables
Leave-one-out TBS avoids overfitting by leaving out more than one observation, becoming k-fold TBS. Ordered TBS avoids overfitting naturally, but suffers from high variance of resulting values, which it tackles by taking a mean over as few iterations as possible. Both methods cause unnecessary overhead.
An alternative approach could be adding noise to the exact values. For example, LOO value mu_0 = k/(N-1) for zero responses and mu_1 = (k-1)/(N-1) for ones. The distance is d = mu_0 – mu_1 = 1/(N-1), so by adding Gaussian noise of e.g. N(mu_0, d) for zero responses and N(mu_1, d) for ones gives at most 69 % accuracy with a best split on a balanced category.
If the standard deviation is capped, e.g. max(0.05, 1/(N-1)), the accuracy would never exceed 69 % for categories smaller than 21 observations and would converge towards 50 % as category size grows, thus becoming similar to greedy target encoding with noise [5].
In comparison to ordered TBS, this approach is faster, simpler, utilizes data as efficiently and avoids overfitting as well. As a bonus, it is not conceptually very far from Beta target encoding, a Bayesian approach.
References
[1] A. V. Dorogush, V. Ershov, A. Gulin. CatBoost: gradient boosting with categorical features support. Workshop on ML Systems at NIPS 2017, 2017.
[2] CatBoost.ai. Transforming categorical features to numerical features. https://catboost.ai/docs/concepts/algorithm-main-stages_cat-to-numberic.html, 2021.
[3] S. Sayad. An Introduction to Data Science. http://www.saedsayad.com/encoding.htm, 2020.
[4] L. Prokhorenkova, G. Gusev, A. Vorobev, A. V. Dorogush, A. Gulin. CatBoost: unbiased boosting with categorical features. arXiv preprint arXiv:1706.09516v2, 2018.
[5] P. Grover. Getting Deeper into Categorical Encodings for Machine Learning. https://towardsdatascience.com/getting-deeper-into-categorical-encodings-for-machine-learning-2312acd347c8, 2019.